Welcome to my new series where I combine the power of Ruby with the discipline of Test-Driven Development (TDD) to tackle popular algorithm problems from LeetCode! 🧑💻💎 Whether you’re a Ruby enthusiast looking to sharpen your problem-solving skills, or a developer curious about how TDD can transform the way you approach coding challenges, you’re in the right place. In each episode, I’ll walk through a classic algorithm problem, show how TDD guides my thinking, and share insights I gain along the way. Let’s dive in and discover how writing tests first can make us better, more thoughtful programmers – one problem at a time! 🚀
🎯 Why I chose this approach
When I decided to level up my algorithmic thinking, I could have simply jumped into solving problems and checking solutions afterward. But I chose a different path – Test-Driven Development with Ruby – and here’s why this combination is pure magic ✨. Learning algorithms through TDD forces me to think before I code, breaking down complex problems into small, testable behaviors. Instead of rushing to implement a solution, I first articulate what the function should do in various scenarios through tests.
This approach naturally leads me to discover edge cases I would have completely missed otherwise – like handling empty arrays, negative numbers, or boundary conditions that only surface when you’re forced to think about what could go wrong. Ruby’s expressive syntax makes writing these tests feel almost conversational, while the red-green-refactor cycle ensures I’m not just solving the problem, but solving it elegantly. Every failing test becomes a mini-puzzle to solve, every passing test builds confidence, and every refactor teaches me something new about both the problem domain and Ruby itself. It’s not just about getting the right answer – it’s about building a robust mental model of the problem while writing maintainable, well-tested code. 🚀
🎲 Episode 1: The Two Sum Problem
#####################################
# Problem 1: The Two Sum Problem
#####################################
# Given an array of integers nums and an integer target, return indices of the two numbers such that they add up to target.
# You may assume that each input would have exactly one solution, and you may not use the same element twice.
# You can return the answer in any order.
# Example 1:
# Input: nums = [2,7,11,15], target = 9
# Output: [0,1]
# Explanation: Because nums[0] + nums[1] == 9, we return [0, 1].
# Example 2:
# Input: nums = [3,2,4], target = 6
# Output: [1,2]
# Example 3:
# Input: nums = [3,3], target = 6
# Output: [0,1]
# Constraints:
# Only one valid answer exists.
# We are not considering following concepts for now:
# 2 <= nums.length <= 104
# -109 <= nums[i] <= 109
# -109 <= target <= 109
# Follow-up: Can you come up with an algorithm that is less than O(n2) time complexity?
🔧 Setting up the TDD environment
Create a test file first and add the first test case.
mkdir two_sum
touch test_two_sum.rb
touch two_sum.rb
# frozen_string_literal: true
require 'minitest/autorun'
require_relative 'two_sum'
###############################
# This is the test case for finding the index of two numbers in an array
# such that adding both numbers should be equal to the target number provided
#
# Ex:
# two_sum(num, target)
# num: [23, 4, 8, 92], tatget: 12
# output: [1, 2] => index of the two numbers whose sum is equal to target
##############################
class TestTwoSum < Minitest::Test
def setup
####
end
def test_array_is_an_empty_array
assert_equal 'Provide an array with length 2 or more', two_sum([], 9)
end
end
Create the problem file: two_sum.rb with empty method first.
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
def two_sum(nums, target)
end
❌ Red: Writing the failing test
Run the test:
ruby test_two_sum.rb
Run options: --seed 58910
# Running:
F
Finished in 0.008429s, 118.6380 runs/s, 118.6380 assertions/s.
1) Failure:
TestTwoSum#test_array_is_an_empty_array [test_two_sum.rb:21]:
--- expected
+++ actual
@@ -1 +1 @@
-"Provide an array with length 2 or more"
+nil
1 runs, 1 assertions, 1 failures, 0 errors, 0 skips
✅ Green: Making it pass
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
def two_sum(nums, target)
'Provide an array with length 2 or more' if nums.empty?
end
♻️ Refactor: Optimizing the solution
❌
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
def two_sum(nums, target)
return 'Provide an array with length 2 or more' if nums.empty?
nums.each_with_index do |selected_num, selected_index|
nums.each_with_index do |num, index|
if selected_index != index
sum = selected_num[selected_index] + num[index]
return [selected_index, index] if sum == target
end
end
end
end
❌
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
def two_sum(nums, target)
return 'Provide an array with length 2 or more' if nums.empty?
nums.each_with_index do |selected_num, selected_index|
nums.each_with_index do |num, index|
next if selected_index == index
sum = selected_num[selected_index] + num[index]
return [selected_index, index] if sum == target
end
end
end
✅
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
def two_sum(nums, target)
return 'Provide an array with length 2 or more' if nums.empty?
nums.each_with_index do |selected_num, selected_index|
nums.each_with_index do |num, index|
next if index <= selected_index
return [selected_index, index] if selected_num + num == target
end
end
end
Final
# frozen_string_literal: true
require 'minitest/autorun'
require_relative 'two_sum'
###############################
# This is the test case for finding the index of two numbers in an array
# such that adding both numbers should be equal to the target number provided
#
# Ex:
# two_sum(num, target)
# num: [23, 4, 8, 92], tatget: 12
# output: [1, 2] => index of the two numbers whose sum is equal to target
##############################
class TestTwoSum < Minitest::Test
def setup
####
end
def test_array_is_an_empty_array
assert_equal 'Provide an array with length 2 or more elements', two_sum([], 9)
end
def test_array_with_length_one
assert_equal 'Provide an array with length 2 or more elements', two_sum([9], 9)
end
def test_array_with_length_two
assert_equal [0, 1], two_sum([9, 3], 12)
end
def test_array_with_length_three
assert_equal [1, 2], two_sum([9, 3, 4], 7)
end
def test_array_with_length_four
assert_equal [1, 3], two_sum([9, 3, 4, 8], 11)
end
def test_array_with_length_ten
assert_equal [7, 8], two_sum([9, 3, 9, 8, 23, 20, 19, 5, 30, 14], 35)
end
end
# Solution 1 ✅
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
def two_sum(nums, target)
return 'Provide an array with length 2 or more elements' if nums.length < 2
nums.each_with_index do |selected_num, selected_index|
nums.each_with_index do |num, index|
already_added = index <= selected_index
next if already_added
return [selected_index, index] if selected_num + num == target
end
end
end
Let us analyze the time complexity of Solution 1 ✅ algorithm:
Our current algorithm is not less than O(n^2) time complexity. In fact, it is exactly O(n^2). This means for an array of length n, you are potentially checking about n(n−1)/2 pairs, which is O(n^2).
🔍 Why?
- You have two nested loops:
- The outer loop iterates over each element (
nums.each_with_index) - The inner loop iterates over each element after the current one (
nums.each_with_index) - For each pair, you check if their sum equals the target.
♻️ Refactor: Try to find a solution below n(^2) time complexity
# Solution 2 ✅
#####################################
# Solution 2
# TwoSum.new([2,7,11,15], 9).indices
#####################################
class TwoSum
def initialize(nums, target)
@numbers_array = nums
@target = target
end
# @return [index_1, index_2]
def indices
return 'Provide an array with length 2 or more elements' if @numbers_array.length < 2
@numbers_array.each_with_index do |num1, index1|
next if num1 > @target # number already greater than target
remaining_array = @numbers_array[index1..(@numbers_array.length - 1)]
num2 = find_number(@target - num1, remaining_array)
return [index1, @numbers_array.index(num2)] if num2
end
end
private
def find_number(number, array)
array.each do |num|
return num if num == number
end
nil
end
end
Let us analyze the time complexity of Solution 2 ✅ algorithm:
- In the
indicesmethod:
- We have an outer loop that iterates through
@numbers_array(O(n)) - For each iteration:
=> Creating a new array sliceremaining_array(O(n)operation)
=> Callingfind_numberwhich isO(n)as it iterates through the remaining array
=> Using@numbers_array.index(num2)which is anotherO(n)operation
So the total complexity is:
O(n)for the outer loop- For each iteration:
O(n)for array slicingO(n)forfind_numberO(n)forindexlookup
This gives us:
O(n * (n + n + n)) = O(n * 3n) = O(3n²) = O(n²)
The main bottlenecks are:
- Creating a new array slice in each iteration
- Using
indexmethod to find the second number’s position - Linear search in
find_number
Solution 3 ✅
To make this truly O(n), we should:
# Use a hash map to store numbers and their indices
# Solution 3 ✅ - Use Hash Map
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
class TwoSum
def initialize(nums, target)
@numbers_array = nums
@target = target
end
# @return [index_1, index_2]
def indices
return 'Provide an array with length 2 or more elements' if @numbers_array.length < 2
hash = {}
@numbers_array.each_with_index do |num, index|
complement = @target - num
# store first number to hash
if index == 0
hash[num] = index
else
# if not first number check store has
return [hash[complement], index] if hash.key?(complement)
# if not found store the num
hash[num] = index
end
end
end
end
Let us analyze the complexity of the current code:
def indices
return 'Provide an array with length 2 or more elements' if @numbers_array.length < 2
hash = {}
@numbers_array.each_with_index do |num, index|
complement = @target - num
# store first number to hash
if index == 0
hash[num] = index
else
# if not first number check store has
if hash.key?(complement)
return [hash[complement], index]
else
# if not found store the num
hash[num] = index
end
end
end
end
The complexity is O(n) because:
- Single pass through the array:
O(n) - For each iteration:
- Hash lookup (
hash.key?(complement)): O(1) - Hash insertion (
hash[num] = index): O(1) - Basic arithmetic (
@target - num): O(1)
Total complexity = O(n) * O(1) = O(n)
The code is still efficient because:
- We only traverse the array once
- All operations inside the loop are constant time
- We don’t have any nested loops or array slicing
- Hash operations (lookup and insertion) are O(1)
♻️ Refactor Solution 3 ✅
This is still O(n):
- Use a hash map to store numbers and their indices
- Avoid array slicing
- Avoid using
indexmethod - Make a single pass through the array
# ♻️ Refactor Solution 3 ✅ - Use Hash Map
# frozen_string_literal: true
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
class TwoSum
def initialize(nums, target)
@numbers_array = nums
@target = target
end
# @return [index_1, index_2]
def indices
return 'Provide an array with length 2 or more elements' if @numbers_array.length < 2
hash = {}
@numbers_array.each_with_index do |num, index|
complement = @target - num
return [hash[complement], index] if hash.key?(complement)
hash[num] = index
end
end
end
This refactored solution has O(n) time complexity because:
- Single pass through the array: O(n)
- Hash operations (insertion and lookup) are O(1)
- No array slicing or linear searches
- Total complexity is O(n)
The algorithm works by:
- For each number, calculate its complement (target – current_number)
- Check if the complement exists in our hash
- If found, return both indices
- If not found, store the current number and its index in the hash
The key differences:
- Instead of searching for complements in the remaining array, we store numbers we’ve seen in a hash
- When we see a new number, we check if its complement exists in our hash
- If found, we return both indices
- If not found, we store the current number and its index
Detailed explanation of refactored solution 3
I’ll explain how the hash map solution works step by step using the example:
# Input Sample
TwoSum.new([2,7,11,15], 9)
- Initial State:
hash = {} # Empty hash map
target = 9
- First Iteration (num = 2, index = 0):
complement = 9 - 2 = 7
hash = {} # Empty, so complement 7 not found
hash[2] = 0 # Store 2 with its index 0
- Second Iteration (num = 7, index = 1):
complement = 9 - 7 = 2
hash = {2 => 0} # Found complement 2 in hash!
return [hash[2], 1] # Returns [0, 1]
Let’s break down what happens in each iteration:
@numbers_array.each_with_index do |num, index|
complement = @target - num # Calculate what number we need
if hash.key?(complement) # Check if we've seen the number we need
return [hash[complement], index] # If found, return both indices
end
hash[num] = index # If not found, store current number and its index
end
Key points:
- We only need to store each number once in the hash
- The hash stores numbers as keys and their indices as values
- We check for complements before storing the current number
- We only need one pass through the array
This is efficient because:
- Hash lookups are O(1)
- We only traverse the array once
- We don’t need to search through the array multiple times
- We don’t need to create array slices
Why the index order has complement index first?
The order of indices in the return statement [hash[complement], index] is important because:
hash[complement]gives us the index of the first number we found (the complement)indexgives us the current position (the second number)
We return them in this order because:
- The complement was stored in the hash earlier in the array
- The current number is found later in the array
- This maintains the order of appearance in the original array
For example, with [2,7,11,15] and target 9:
- When we see
7at index1:
- We look for complement
2(9-7) 2was stored at index0- So we return
[0, 1](indices of[2,7])
If we returned [index, hash[complement]], we would get [1, 0] instead, which would be the reverse order. While the problem allows returning the answer in any order, returning them in the order they appear in the array is more intuitive and matches the example outputs in the problem description.
✅ Solution 4
# Solution 4 ✅ - Use Hash Map
# @param {Integer[]} nums
# @param {Integer} target
# @return {Integer[]}
def two_sum(nums, target)
return 'Provide an array with length 2 or more elements' if nums.length < 2
# number index store, use hash map, store first number in store
store = { nums[0] => 0}
# check the pair from second element
nums.each_with_index do |num, index|
next if index == 0 # already stored first
pair = target - num
return [store[pair], index] if store[pair]
store[num] = index
end
end
Check my LeetCode progress:
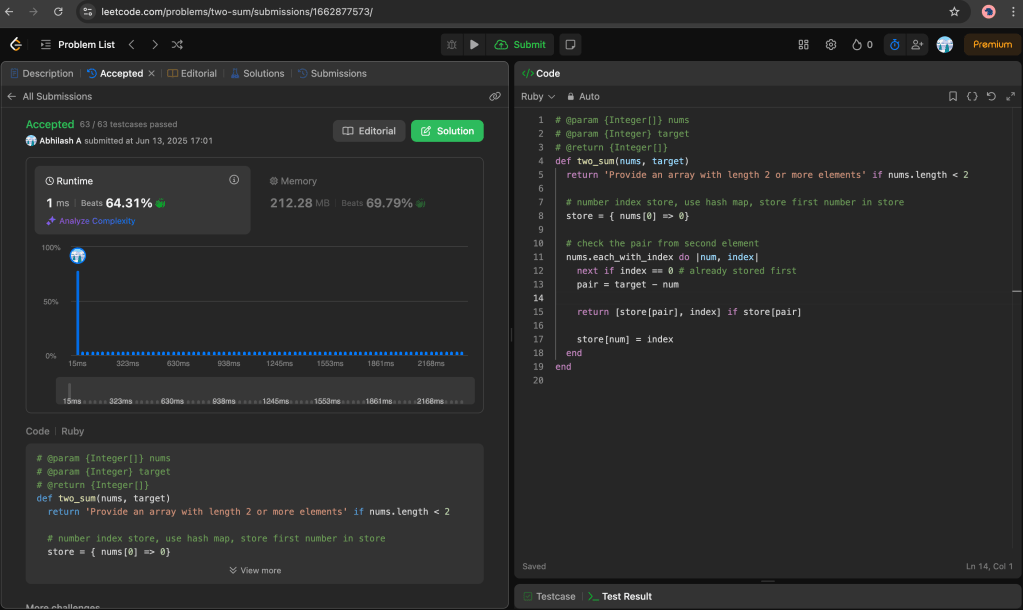
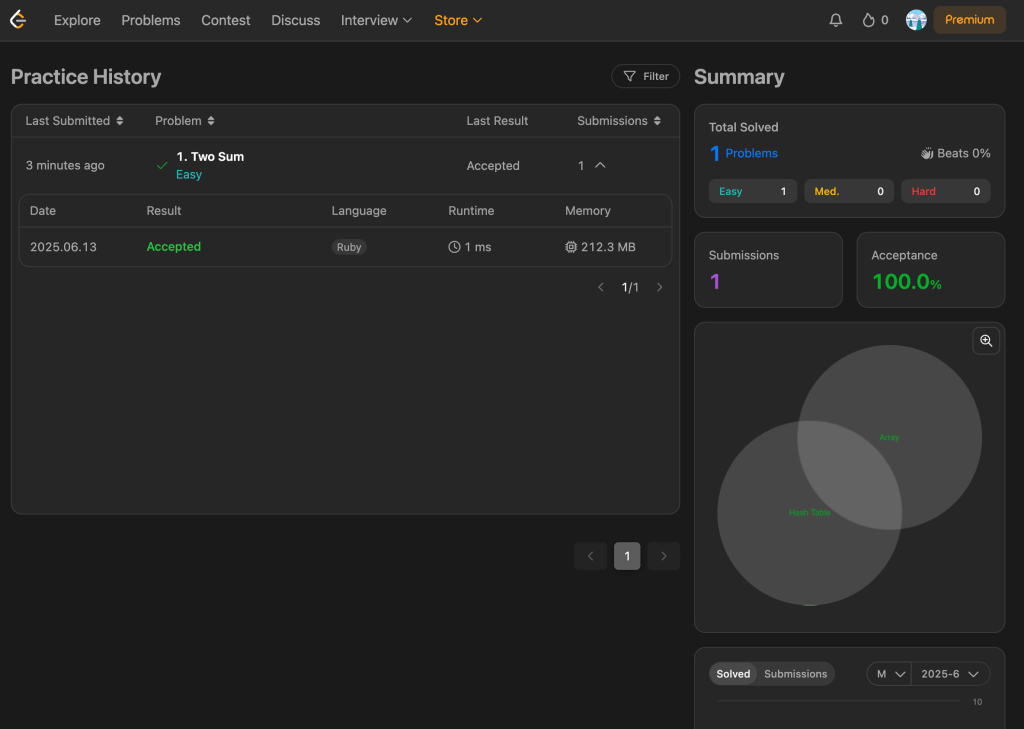
The Problem: https://leetcode.com/problems/two-sum/description/
Solution: https://leetcode.com/problems/two-sum/submissions/1662877573/
🧠 Lessons learned
- Solution 1 ✅ – We found our first solution which is working fine. But has
o(n^2) - Solution 2 ✅ – We refactored and found our second solution which is working fine. But also has
o(n^2) - Solution 3 ✅ – We refactored to hash_map which is working fine and has time complexity
o(n)! 💥
Happy Algo Coding! 🚀
