🏃‍♂️ Solving LeetCode Problems the TDD Way (Test-First Ruby): Best Time to Buy and Sell Stock


Welcome to my new series where I combine the power of Ruby with the discipline of Test-Driven Development (TDD) to tackle popular algorithm problems from LeetCode! 🧑‍💻💎 Whether you’re a Ruby enthusiast looking to sharpen your problem-solving skills, or a developer curious about how TDD can transform the way you approach coding challenges, you’re in the right place.

🎲 Episode 2: Best Time to Buy and Sell Stock

###############################################
#   Problem 2: Best Time to Buy and Sell Stock
###############################################

You are given an array prices where prices[i] is the price of a given stock on the ith day.

You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.

Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.


Example 1:

Input: prices = [7,1,5,3,6,4]
Output: 5
Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.
Example 2:

Input: prices = [7,6,4,3,1]
Output: 0
Explanation: In this case, no transactions are done and the max profit = 0.
 

Constraints:

1 <= prices.length <= 105
0 <= prices[i] <= 104

🔧 Setting up the TDD environment

Create files and folder

mkdir buy_sell_stock
touch buy_sell.rb
touch test_buy_sell.rb

# frozen_string_literal: true

require 'minitest/autorun'
require_relative 'buy_sell'
#####################
##
#####################
class TestBuySell < Minitest::Test
  def setup
  end

  # ex: []
  def test_array_is_an_empty_array
  end
end


########################
# @param {Integer[]} prices
# @return {Integer}
# Ex: max_profit([])
def max_profit
end

❌ Red: Writing the failing test

# frozen_string_literal: true

# ❌ first failing test case
require 'minitest/autorun'
#####################
##
#####################
class TestBuySell < Minitest::Test
  def setup
    ####
  end

  # ex: []
  def test_array_is_an_empty_array
    assert_equal 'Provide an array of two or more elements', []
  end
end


 ✗ ruby buy_sell_stock/test_buy_sell.rb
Run options: --seed 46112

# Running:
E
Finished in 0.000438s, 2283.1050 runs/s, 0.0000 assertions/s.

  1) Error:
TestBuySellStock#test_array_is_an_empty_array:
NameError: uninitialized constant TestBuySellStock::BuySellStock
    buy_sell_stock/test_buy_sell.rb:19:in 'TestBuySellStock#test_array_is_an_empty_array'

1 runs, 0 assertions, 0 failures, 1 errors, 0 skips

✅ Green: Making it pass

########################
# @param {Integer[]} prices
# @return {Integer}
# Ex: max_profit([])
def max_profit
    'Provide an array of two or more elements' if @prices.empty?
end

…………………………………………………. ⤵ …………………………………………………………..

Writing the Second Test Case:

# frozen_string_literal: true

# ❌ second failing test case
require 'minitest/autorun'
#####################
##
#####################
class TestBuySell < Minitest::Test
  def setup
    ####
  end

  # ex: []
  def test_array_is_an_empty_array
    assert_equal 'Provide an array of two or more elements', []
  end

  def test_array_with_length_one
    assert_equal 'Provide an array of two or more elements', [1]
  end 
end


########################
# @param {Integer[]} prices
# @return {Integer}
# Ex: BuySellStock.new([2,8]).max_profit
def max_profit
    'Provide an array of two or more elements' if @prices.length < 2
end

…………………………………………………. ⤵ …………………………………………………………..

Writing the Third, Fourth Test Case:

# frozen_string_literal: true

require 'minitest/autorun'
require_relative 'buy_sell'
#####################
##
#####################
class TestBuySellStock < Minitest::Test
  def setup
    ####
  end

  def create_array(length)
    Array.new(length) { rand(1..100) }
  end

  # ex: BuySellStock.new([]).max_profit
  def test_array_is_an_empty_array
    assert_equal 'Provide an array of two or more elements', BuySellStock.new([]).max_profit
  end

  def test_array_with_length_one
    assert_equal 'Provide an array of two or more elements', BuySellStock.new([1]).max_profit
  end

  def test_array_with_length_two
    assert_equal 2, BuySellStock.new([1, 3]).max_profit
    assert_equal 0, BuySellStock.new([5, 3]).max_profit
  end

  def test_array_with_length_three
    assert_equal 5, BuySellStock.new([1, 3, 6]).max_profit
    assert_equal 0, BuySellStock.new([5, 3, 2]).max_profit
  end
end


Solution 1 ✅
########################
# @param {Integer[]} prices
# @return {Integer}
# Ex: BuySellStock.new([2,8]).max_profit
########################
class BuySellStock
  def initialize(prices)
    @prices = prices
    @profit_store = {}
  end

  def max_profit
    return 'Provide an array of two or more elements' if @prices.length < 2

    # iterate today's price
    @prices.each_with_index do |todays_price, index|
      # check profit with future prices
      @prices[(index + 1)..].each do |future_price|
        profit = future_price - todays_price
        update_profit_store(index, profit) if profit.positive?
      end
    end

    @profit_store.values.max || 0
  end

  def update_profit_store(index, profit)
    @profit_store[index] = 0 unless @profit_store[index]

    @profit_store[index] = profit if profit > @profit_store[index]
  end
end

⏳ Finding the Time Complexity

Let me analyze the time complexity of your algorithm in buy_sell.rb.

Looking at our code, there are two nested loops:

  1. The outer loop iterates through each price in the array using each_with_index
  2. The inner loop iterates through all future prices using @prices[(index + 1)..]

For an array of length n:

  • The outer loop runs n times
  • For each iteration of the outer loop, the inner loop runs (n-1), (n-2), (n-3), …, 1 times

This creates a pattern of:

  • First iteration: n-1 comparisons
  • Second iteration: n-2 comparisons
  • Third iteration: n-3 comparisons
  • And so on…

This is equivalent to the sum of the first (n-1) natural numbers:
(n-1) + (n-2) + (n-3) + … + 1 = n(n-1)/2

Therefore, the time complexity is O(n²) or quadratic time complexity.

The space complexity is O(n) because:

  • We store the prices array: O(n)
  • We store the profit_store hash which in worst case could store n-1 entries: O(n)

💡 Tip: To optimize this, we could use a single pass approach that keeps track of the minimum price seen so far and calculates the maximum profit in one iteration, which would give you O(n) time complexity.

♻️ Refactor: Optimizing the solution

Let’s optimize the algorithm step by step. Modify our code to achieve O(n) time complexity.

The key insight is that we only need to:

  1. Keep track of the minimum price we’ve seen so far
  2. For each price, calculate the potential profit if we sell at current price
  3. Update the maximum profit if current profit is higher

Here’s how we’ll modify your code:

Let me explain the optimization step by step:

  1. First, we remove the @profit_store hash since we don’t need it anymore:
def initialize(prices)
  @prices = prices
end
  1. In the max_profit method, we’ll use two variables:
  • min_price: to keep track of the lowest price we’ve seen so far
  • max_profit: to keep track of the maximum profit we can make
  1. The optimized algorithm snippet looks like this (Check: Final Solution ✅ at the bottom):
def max_profit
  return 'Provide an array of two or more elements' if @prices.length < 2

  min_price = @prices[0]  # Start with first price as minimum
  max_profit = 0          # Start with 0 profit

  @prices.each do |price|
    # Update min_price if current price is lower
    min_price = [min_price, price].min

    # Calculate potential profit
    potential_profit = price - min_price

    # Update max_profit if current profit is higher
    max_profit = [max_profit, potential_profit].max
  end

  max_profit
end

Let’s walk through how this works with the example [7,1,5,3,6,4]:

the optimized algorithm I described above works perfectly for this problem! Let me explain why:

The Problem Requirements:

  1. Choose a single day to buy one stock
  2. Choose a different day in the future to sell that stock
  3. Maximize profit from this transaction
  4. Return 0 if no profit is possible

How the Optimized Algorithm Satisfies These Requirements:

  1. Single buy/sell transaction: ✅ The algorithm finds the best single buy-sell pair
  2. Buy before sell: ✅ As we iterate through the array, min_price always represents a price from a previous day (or current day), ensuring we buy before we sell
  3. Maximize profit: ✅ We keep track of the maximum profit seen so far
  4. Return 0 if no profit: ✅ We initialize max_profit = 0 and only update it if we find a positive profit

Key Insight:

The algorithm works because at any given day, the maximum profit we can achieve by selling on that day is: current_price - minimum_price_seen_so_far

Since we process prices chronologically, the minimum price we’ve seen so far is always from a previous day (or the same day), which satisfies the “buy before sell” constraint.

  1. Start with min_price = 7 and max_profit = 0
Example with [7,1,5,3,6,4]:
Day 0: price=7, min_price=7, profit=0
Day 1: price=1, min_price=1, profit=0
Day 2: price=5, min_price=1, profit=4 (buy day 1, sell day 2)
Day 3: price=3, min_price=1, profit=2 (buy day 1, sell day 3)
Day 4: price=6, min_price=1, profit=5 (buy day 1, sell day 4) ← Maximum
Day 5: price=4, min_price=1, profit=3 (buy day 1, sell day 5)

The algorithm correctly identifies buying on day 1 (price=1) and selling on day 4 (price=6) for maximum profit of 5.

The time complexity is now O(n) because:

  • We only make a single pass through the array
  • Each operation inside the loop is O(1)
  • No nested loops

The space complexity is O(1) because:

  • We only use two variables regardless of input size
  • We don’t store any additional data structures
Your Current Algorithm vs Optimized:
  • Your current O(n²) algorithm: Works correctly but inefficient
  • Optimized O(n) algorithm: Works correctly and much more efficient

Both solve the same problem correctly, but the optimized version is significantly faster for large inputs.

♻️ Refactor: Try to find a solution below o(n^2) time complexity

# Solution 2 ✅ - Final Solution submitted
# frozen_string_literal: true

##########################################
#
# You are given an array prices where prices[i] is the price of a given stock on the ith day.
# You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
# Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
# Example 1:
# Input: prices = [7,1,5,3,6,4]
# Output: 5
# Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
# Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

# Example 2:
# Input: prices = [7,6,4,3,1]
# Output: 0
# Explanation: In this case, no transactions are done and the max profit = 0.
#
#  Constraints:
# 1 <= prices.length <= 105
# 0 <= prices[i] <= 104
##########################################
# @param {Integer[]} prices
# @return {Integer}
# Ex: BuySellStock.new([2,8]).max_profit
class BuySellStock
  def initialize(prices)
    @prices = prices
    @profit_store = {}
  end

  def max_profit
    return 'Provide an array with 1 or more elements' if @prices.empty?

    max_profit = 0 # Start with 0 profit
    return max_profit if @prices.length == 1

    lowest_price = @prices.first # assume lowest price is the first price
    @prices.each do |current_price|
      current_profit = current_price - lowest_price
      max_profit = current_profit  if current_profit > max_profit
      lowest_price = current_price if current_price < lowest_price
    end

    max_profit
  end
end


##########
# Solution 3 ✅ - For Reference by AI
# frozen_string_literal: true

##########################################
#
# You are given an array prices where prices[i] is the price of a given stock on the ith day.
# You want to maximize your profit by choosing a single day to buy one stock and choosing a different day in the future to sell that stock.
# Return the maximum profit you can achieve from this transaction. If you cannot achieve any profit, return 0.
# Example 1:
# Input: prices = [7,1,5,3,6,4]
# Output: 5
# Explanation: Buy on day 2 (price = 1) and sell on day 5 (price = 6), profit = 6-1 = 5.
# Note that buying on day 2 and selling on day 1 is not allowed because you must buy before you sell.

# Example 2:
# Input: prices = [7,6,4,3,1]
# Output: 0
# Explanation: In this case, no transactions are done and the max profit = 0.
#
#  Constraints:
# 1 <= prices.length <= 105
# 0 <= prices[i] <= 104
##########################################
# @param {Integer[]} prices
# @return {Integer}
# Ex: BuySellStock.new([2,8]).max_profit
class BuySellStock
  def initialize(prices)
    @prices = prices
    @profit_store = {}
  end

  def max_profit
    return 'Provide an array with 1 or more elements' if @prices.empty?

    max_profit = 0          # Start with 0 profit
    return max_profit       if @prices.length == 1

    min_price = @prices[0]  # Start with first price as minimum

    @prices.each do |price|
      # Update min_price if current price is lower
      min_price = [min_price, price].min

      # Calculate potential profit
      potential_profit = price - min_price

      # Update max_profit if current profit is higher
      max_profit = [max_profit, potential_profit].max
    end

    max_profit
  end
end

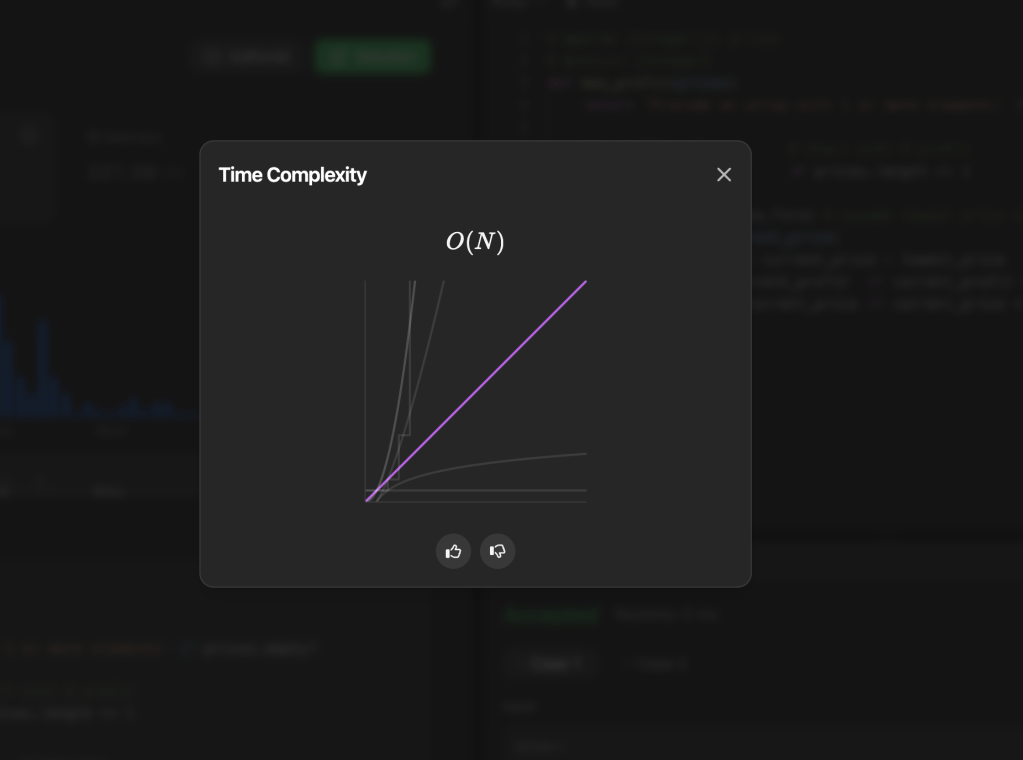
Time Complexity: O(n) ✅

About the time complexity being O(n). Here’s why:

  • You have a single loop that iterates through the @prices array once: @prices.each do |current_price|
  • Inside the loop, all operations are O(1):
  • current_profit = current_price – lowest_price → O(1)
  • max_profit = current_profit if current_profit > max_profit → O(1)
  • lowest_price = current_price if current_price < lowest_price → O(1)
  • No nested loops, no recursive calls
  • Total: O(n)

Space Complexity: O(1) – Not O(n)

It’s actually O(1) constant space, not O(n). Here’s why:

Space used:

  • max_profit variable → O(1)
  • lowest_price variable → O(1)
  • current_price (loop variable) → O(1)
  • current_profit variable → O(1)
  • The @prices array → This is input data, not additional space used by the algorithm
  • @profit_store → You’re not using this anymore in the optimized version

Key Point: In space complexity analysis, we typically don’t count the input data itself. We only count the additional space the algorithm uses beyond the input. Since you’re only using a constant number of variables (4 variables) regardless of the input size, the space complexity is O(1).

Summary:

  • Time Complexity: O(n) ✅
  • Space Complexity: O(1) (not O(n))

…………………………………………………. ⤵ …………………………………………………………..

The Problem: https://leetcode.com/problems/best-time-to-buy-and-sell-stock/

The Solution: https://leetcode.com/problems/best-time-to-buy-and-sell-stock/submissions/1663843909/

Happy Algo Coding! 🚀

Unknown's avatar

Author: Abhilash

Hi, I’m Abhilash! A seasoned web developer with 15 years of experience specializing in Ruby and Ruby on Rails. Since 2010, I’ve built scalable, robust web applications and worked with frameworks like Angular, Sinatra, Laravel, Node.js, Vue and React. Passionate about clean, maintainable code and continuous learning, I share insights, tutorials, and experiences here. Let’s explore the ever-evolving world of web development together!

Leave a comment